設計探討 | 圓鋼管混凝土的界限套箍系數
瀏覽次數：1798次發布時間：2023/06/12
編者按
近三十年來各種類型的鋼結構在我國獲得了大范圍的應用,其快速發展促進了對它們設計方法的研究。由于研究手段的現代化,鋼結構穩定理論、抗震設計理論和組合結構理論都取得了巨大的進展,鋼結構及其配套新技術也不斷出現。雖然鋼結構應用廣泛,鋼結構設計規范也已經進入第 4 個版本即 2017 版本,但是鋼結構設計仍存在很多亟待改進的地方,例如外露式柱腳的錨栓能否參與抗剪以及抗剪承載力如何計算,外包式柱腳的外包混凝土層是鋼柱的支座還是與鋼柱共同工作形成了鋼骨混凝土(SRC)柱,抗震結構的梁柱節點域應設計成強節點域還是弱節點域,等等。浙江大學童根樹教授在參與鋼結構相關規范的過程中對這些問題進行了一些思考,并帶領團隊進行了相關深入研究,在重視理論的同時也偏向工程應用,積累了很多很好的設計經驗。為進一步促進和推動我國鋼結構設計方法和技術的發展,《鋼結構(中英文)》編輯部特邀童根樹教授將其在鋼結構設計研究中的新觀點、新方法和新結果進行系列介紹,以饗讀者,并歡迎大家交流和探討。
摘要
簡要論述了圓鋼管混凝土短柱性能的一個重要方面：界限套箍系數的理論確定方法，采用該方法計算的結果與已有試驗結果符合，表明本文提出方法的基本合理性。
1 什么是界限套箍系數
界限套箍系數是鋼管混凝土短柱的軸壓力-軸向應變曲線不出現下降段時的套箍系數，圖1引自Tomii等1979年的研究報告。本文提出一個求解界限套箍系數的理論方法。
圖1 鋼管混凝土短柱壓力-應變關系
2 鋼和混凝土簡單相加獲得的曲線
鋼與混凝土簡單相加的壓力-軸向應變曲線如圖2。圖中 N0 是圓鋼管混凝土鋼材屈服強度和混凝土棱柱強度簡單相加的承載力，圖片是套箍系數：
式中：As、Ac 分別為鋼材和混凝土的面積；fy、fpr 分別為鋼材屈服強度和混凝土棱柱強度。
采用 GB50010-2016《混凝土結構設計規范》附錄中的混凝土應力應變曲線，鋼材采用接近理想彈塑性的曲線，因為圖2中最大應變為2%，鋼材應力應變進入強化階段很小。
圖2 簡單相加時壓力-應變關系
提取簡單相加的曲線峰值后的下降段的最小承載力比值（圖2），擬合公式得到：
式中:圖片為圓鋼管混凝土短柱受壓承載力相對于簡單相加承載力的提高系數。由圖2可知，最小剩余承載力出現的應變為1.5%~ 1.85%，而承載力峰值出現的應變在0.2%附近。
圖2的簡單相加曲線與圖1曲線有巨大差別，圖１的試驗曲線把圖2所示簡單相加曲線的下降部分消除了，這是因為鋼管對混凝土的環向約束作用，即套箍作用。
被圓鋼管套箍作用填平的曲線高差是：
3 界限套箍系數的求解
套箍作用使鋼與混凝土界面上產生了圍壓，記為 p 。鋼管則產生環向拉力，豎向屈服承載力下降。采用Mises屈服準則，鋼管豎向承載力的下降部分為：
式中：t 為鋼管壁厚，Dc 為混凝土直徑。
鋼管內的核心混凝土承受水平圍壓后的強度記為 fpr,p，國際上計算這個強度的公式都是混凝土圓柱試件液壓施加圍壓后再豎向加載得到抗壓強度，這種試驗是主動圍壓試驗。鋼管內混凝土的應力加載路徑不同，開始時沒有圍壓，然后混凝土開裂膨脹產生圍壓，但后期混凝土密實度增加，經過大量試算發現，應變達到 1.5%~1.85%,被動圍壓 p 時混凝土強度為：
管內混凝土承載力的增加部分是：
套箍作用能夠填平圓鋼管混凝土壓力-應變曲線，核心混凝土承載力的增加部分減去鋼管承載力的下降部分，應等于式(4)這一承載力的下降量，即：
于是得到一代數方程。
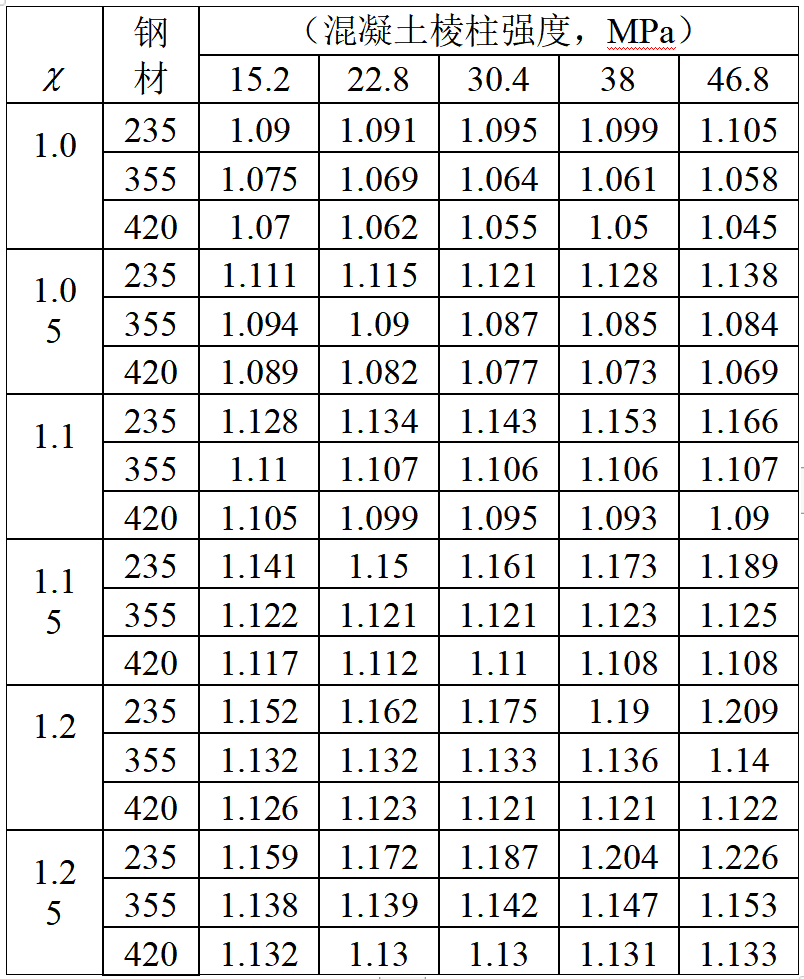
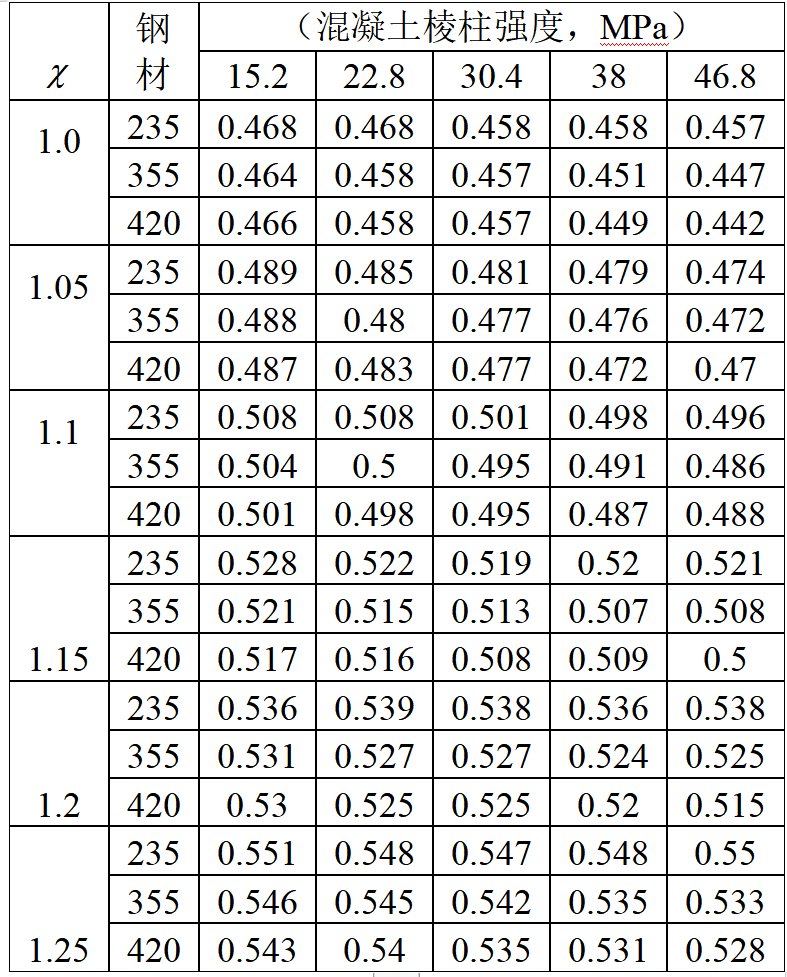
給定圖片，由式(8)可解出 p/fpr，套箍系數小時式(8)無解,表示套箍系數小時無法填平曲線。表1給出結果，與相關文獻上介紹的試驗結果界限套箍系數約為1.12基本符合。
表1 界限套箍系數
表2 圍壓 p/fpr
本文介紹了計算界限套箍系數的一種理論方法，理論解與試驗結果基本一致，說明式(5)是一個合適的式子。
計算鋼管混凝土短柱承載力時圍壓和豎向強度（對應的應變在0.25%~0.3%）的關系是：
式(5)的圍壓效率系數3.36（式(5)的第2項）比式(9)系數2.603提高了30%~60％,表明荷載-應變曲線在越過承載力點后，隨著豎向應變的增加，圍壓效率系數在增加。
4 結束語
本文介紹了計算界限套箍系數的一種理論方法，界限套箍系數值 1.0~1.1 之間，理論解與試驗結果基本一致，說明式(5)是一個合適的式子，適用于應變在1.5％～1.85%時。式(5)的系數大于式(9)的系數，表明隨著軸向應變從0.2％增加到1.5%~1.85%，圍壓效率系數在增加。
來源
童根樹. 圓鋼管混凝土的界限套箍系數[J]. 鋼結構(中英文)202338(6): 61-63.
文章轉自公眾號鋼結構
如有侵權，請聯系我們刪除
0898-66756178
18889805710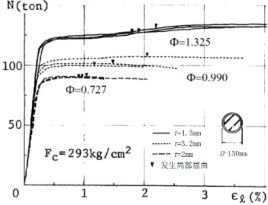
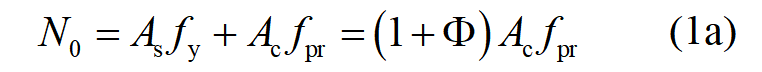
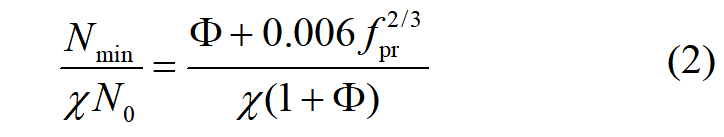
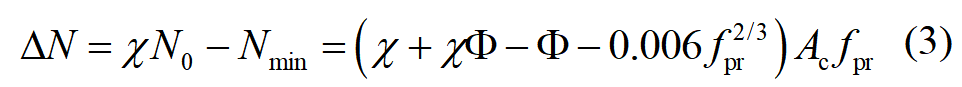
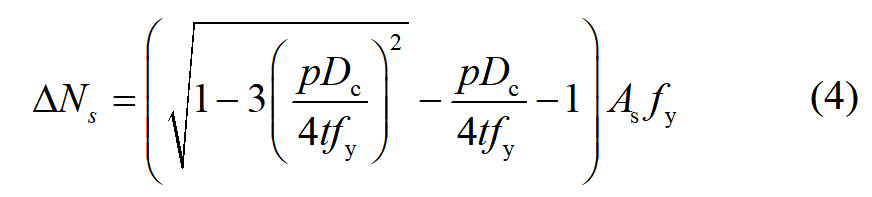
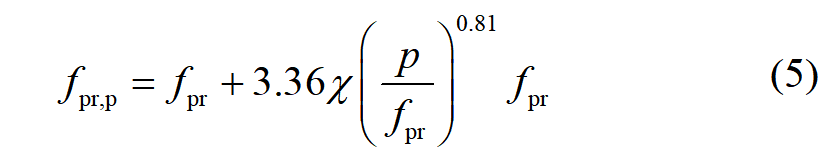
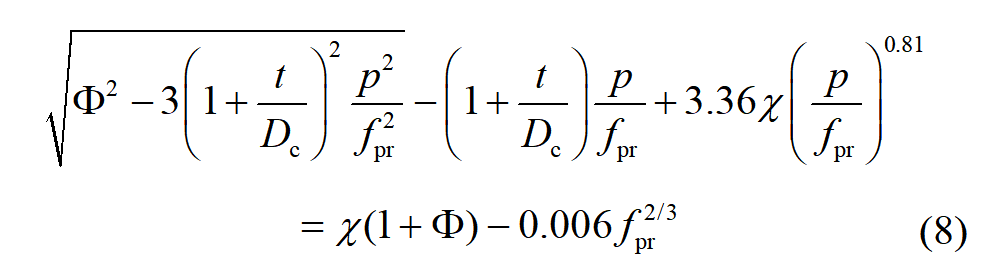
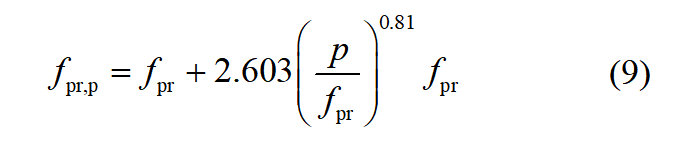
0898-66756178
18889805710